Previsioni, pronostici con la matrice di transizione Markoviana
LOTTERIE: LOTTO, SUPER ENALOTTO, 10 E LOTTO, EUROJACKPOT, MILLIONDAY
Introduzione
Le catene di Markov sono modelli matematici che descrivono sistemi che evolvono passo dopo passo da uno stato al successivo, secondo regole puramente probabilistiche. Ciò che le caratterizza è la proprietà di Markov, o “memoria corta”: la probabilità di trovarsi in un certo stato dipende soltanto dallo stato immediatamente precedente, non da tutta la storia passata.
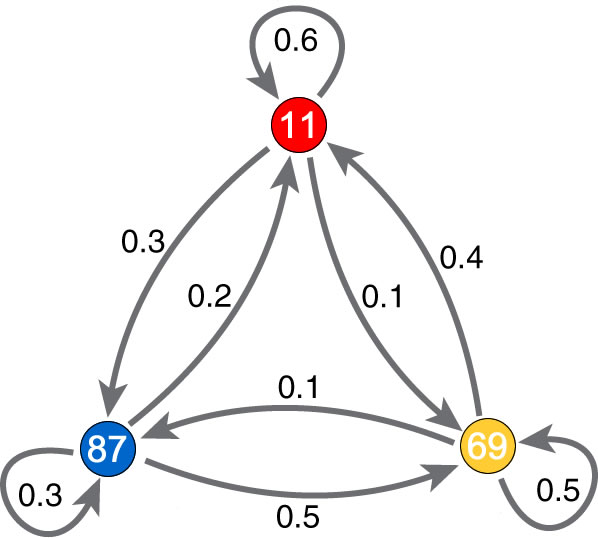
Per ogni coppia di stati (ad es. “è uscito il numero A” → “poi è uscito il numero B”) si calcola quante volte, nei dati storici di estrazione, quel passaggio si è effettivamente verificato. Questi conteggi vengono normalizzati e organizzati in una matrice di transizione:
- le righe corrispondono allo stato di partenza,
- le colonne allo stato di arrivo,
- la cella (i,j) contiene la probabilità stimata di passare dallo stato i a quello j.
In pratica, se per la ruota di Milano storicamente dal numero 17 è seguito il 32 in 15 estrazioni su 100, nella matrice alla riga 17 e colonna 32 troveremo 0.15 (15%).
Applicando ripetutamente questa logica a una sequenza di estrazioni, otteniamo un modello che riflette le tendenze “locali” del sistema: pur restando un gioco d’azzardo, la catena di Markov ci aiuta a individuare i passaggi (e quindi i numeri) statisticamente più “naturali”.

Metodo NEXT NUMBER
Il metodo Next Number lavora sfruttando la matrice di transizione costruita sulle estrazioni precedenti.
A partire dai numeri dell’ultima estrazione, il sistema segue i collegamenti nella matrice per cercare i numeri che hanno più probabilità di “succedere” a quelli appena usciti.
Ad ogni passo, la catena si evolve:
- Se un numero ha diversi successori possibili, il sistema sceglie casualmente, ma rispettando le probabilità indicate nella matrice.
- Se invece un numero non ha successori (ovvero, tutte le probabilità sono nulle), la catena si interrompe.
Questo processo genera più catene possibili, che rappresentano gli scenari più probabili di evoluzione futura.
Analizzando queste catene, possiamo individuare i numeri più ricorrenti (“numeri caldi”) o quelli più isolati (“numeri freddi”), utili per tentare previsioni mirate.
Metodo TRANSITION NUMBERS
Il metodo Transition Numbers lavora in modo diverso:
anziché seguire un percorso specifico, calcola come si distribuiscono le probabilità su tutti i numeri ad ogni passo futuro.
Immagina di “proiettare in avanti” l’intera situazione attuale:
- Partendo dai numeri appena estratti, la matrice viene applicata più volte.
- A ogni passo (T+1, T+2, T+3…) otteniamo un nuovo insieme di probabilità distribuite su tutti i numeri.
Questa tecnica non crea una storia, ma dà una vista d’insieme di quali numeri stanno diventando statisticamente più forti o più deboli man mano che il tempo (e le estrazioni) avanzano.
Qualche consiglio pratico riguardo al metodo TRANSITION NUMBERS
- Con pochi dati storici, il sistema è molto reattivo ma meno affidabile (può dare indicazioni “brillanti” ma casuali).
- Con troppi dati, la matrice tende ad appiattirsi: le probabilità si livellano e i numeri si comportano come in un’estrazione casuale.
Il trucco è trovare un buon equilibrio:
né troppo poco, né troppo storico.
In genere, usare 200-400 estrazioni recenti offre una base solida per avere sia trend attuali che coerenza statistica.
TI PIACE QUESTO PROGETTO? AIUTAMI A MANTENERLO IN VITA DONANDO IL TUO CONTRIBUTO. GRAZIE.
I dati statistici ed eventuali pronostici, metodi e/o sistemi sono forniti da Lotto I.A. a solo titolo di studio, non si invita al gioco reale. Non si vuole in nessun caso istigare al gioco d’azzardo. Non si garantisce in nessun modo alcuna vincita. Gli autori non possono essere considerati in alcun modo responsabili di perdite finanziarie. Gioca consapevole!
